Die Teilkreisexzentrizität besteht, wenn das Drehzentrum A der Alhidade (entspricht Stehachse) nicht mit dem Mittelpunkt M des Teilkreises zusammenfällt. In diesem Fall liegt eine Exzentrizität e vor. Diese kann unabhängig bei beiden Teilkreisen (Horizontal- und Vertikalteilkreis) auftreten.
Ursache: Unvermeidliche Abweichung bei der feinmechanischen Fertigung und Montage
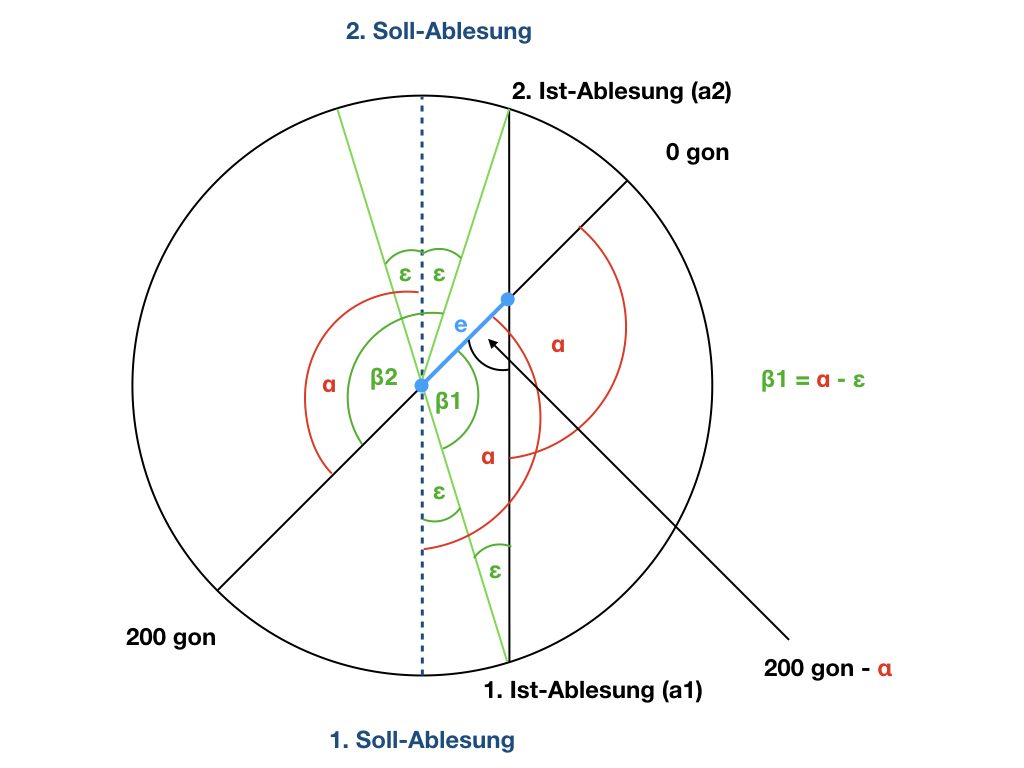
e = Teilkreisexzentrizität
– – – = Soll-Ablesung ohne Exzentrizität
— = Ist-Ablesung mit Exzentrizität
ε = Abweichung der Winkel- bzw. Richtungsmessung
β1 = abgelesener Ist-Winkel bzw. Ist-Richtung 1. Lage
β2 = abgelesener Ist-Winkel bzw. Ist-Richtung 2. Lage
α = Soll-Winkel bzw. Soll-Richtung gesamt
Wichtige Formeln
Abgelesene Richtung = Soll-Richtung – Abweichung
Dreieck M-A-a1 (in der Zeichnung e-a1) mit Sinus-Satz:
Der Sinus hat bei 100 gon ein Maximum. Rechts und links davon verläuft der Sinus gespiegelt. Aus diesem Grund entspricht .
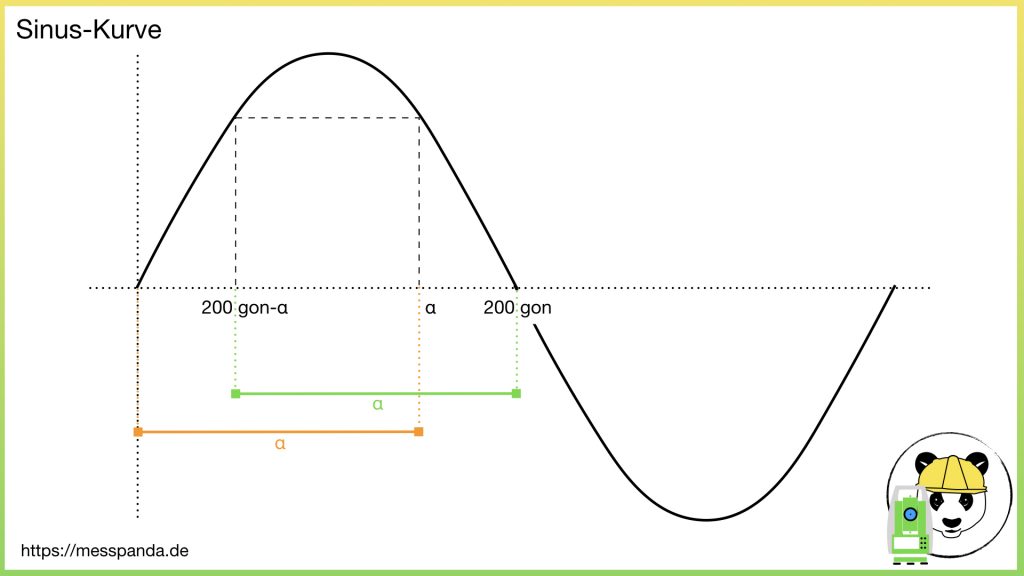
Berechnung der Soll-Richtung α:
I: 1. Ist-Ablesung:
II. 2. Ist-Ablesung:
III. 1 in 2 eingesetzt:
Elimination der Teilkreisexzentrizität
- Messen in zwei Lagen
Wichtig: Die Teilkreisexzentrizität fällt nur beim Horizontalkreis durch Messen in zwei Lagen heraus. Beim Vertikalkreis fällt der Einfluss e nicht durch das Messen in zwei Lagen heraus, weil die Ablesung hier nicht diametral ist.
Bei modernen Tachymetern wird Abhilfe geschaffen, indem mehrere (z.B. vier gegenüberliegende) Winkelencoder eingesetzt werden. Wenn der Teilkreis nun exzentrisch zu den Winkelencodern ist, lesen diese teilweise zu große und teilweise zu kleine Winkel ab. Durch eine Mittelung gleichen sich die Werte weitgehend aus. Die Teilkreisexzentrizität wird so automatisch reduziert. (→ Themenbereich Industrielle Messtechnik).
Typische Klausuraufgaben:
Der Einfluss der Teilkreisexzentrizität (vertikal) fällt beim Messen in 2 Lagen nicht raus.
— Ja.
Der Einfluss der Teilkreisexzentrizität (horizontal) fällt beim Messen in 2 Lagen nicht raus.
— Nein.
Literaturhinweis: Deumlich/Staiger (2002) Instrumentenkunde der Vermessungstechnik

